2D-поворот в WebGL

1. Що таке радіани?

Ця стаття з серії, яка починається з основ WebGL , Є продовженням попередньої статті про перенесення геометрії .

Мушу визнати, що не маю поняття, як мені все це пояснити і донести сенс, але хіба така дрібниця зможе мене зупинити? ..

Для початку я хочу познайомити вас з так званої "одиничною окружністю". Якщо ви пам'ятаєте математику середньої школи (так-так, і не смійте тут засипати!), Окружність має радіус. Радіус кола - це відстань від центру кола до її кордону. Одиничне коло - це коло з радіусом, рівним одиниці.

Ось та сама одиничне коло.

Якщо ви потягнете за синій кружок навколо кола, значення X і Y будуть змінюватися. Вони представляють положення точки на колі. На самому верху Y дорівнює 1, а X дорівнює 0. Справа X дорівнює 1, а Y дорівнює 0.

З того ж курсу шкільної математики ви, мабуть, пам'ятаєте, що якщо значення помножити на одиницю, воно не зміниться. Тобто 123 * 1 = 123. Досить просто, правда? В якомусь сенсі одиничне коло - теж свого роду одиниця. Одиниця для обертання. Тобто ви можете помножити що-небудь на одиничну окружність, і це буде схоже на множення на одиницю, тільки ще відбудеться магія і об'єкт повернеться.

Ми візьмемо значення X і Y з будь-якої точки одиничного кола, і помножимо на них нашу геометрію з попереднього прикладу .

У шейдера відбудуться такі зміни:

<Script id = "2d-vertex-shader" type = "x-shader / x-vertex"> attribute vec2 a_position; uniform vec2 u_resolution; uniform vec2 u_translation; + Uniform vec2 u_rotation; void main () {+ // Поворот вершини + vec2 rotatedPosition = vec2 (+ a_position.x * u_rotation.y + a_position.y * u_rotation.x, + a_position.y * u_rotation.y - a_position.x * u_rotation.x) ; // Потім перенесення * vec2 position = rotatedPosition + u_translation;

Змінимо JavaScript, щоб можна було передати ці 2 значення.

... + var rotationLocation = gl.getUniformLocation (program, "u_rotation"); ... + var rotation = [0, 1]; ... // Отрісовка сцени function drawScene () {... // Задаємо перенесення gl.uniform2fv (translationLocation, translation); + // Задаємо обертання + gl.uniform2fv (rotationLocation, rotation); // отрісовиваємих геометрію var primitiveType = gl.TRIANGLES; var offset = 0; var count = 18; // буква "F" з 6 трикутників, 3 точки на трикутник gl.drawArrays (primitiveType, offset, count); }

І отримуємо результат. Потягніть за синій кружок на окружності для повороту або за слайдери для перенесення.

Як це працює? Погляньмо на математику.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x; rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Скажімо, у нас є прямокутник, який потрібно перевернути. Спочатку його верхній правий кут знаходиться в координатах 3.0, 9.0. Тепер візьмемо точку на одиничному колі, зміщеною на 30 градусам від 12 годині за годинниковою стрілкою.

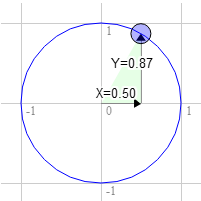
Положення на окружності в цьому місці буде мати значення 0.50 і 0.87.

3.0 * 0.87 + 9.0 * 0.50 = 7.1 9.0 * 0.87 - 3.0 * 0.50 = 6.3

Саме тут нам і потрібно бути.

Те ж саме для 60 градусів за годинниковою стрілкою.

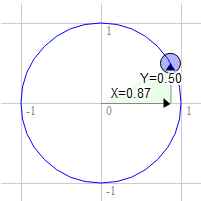
Положення на окружності в цьому місці буде мати значення 0.87 і 0.50

3.0 * 0.50 + 9.0 * 0.87 = 9.3 9.0 * 0.50 - 3.0 * 0.87 = 1.9

Ви можете помітити, що з поворотом за годинниковою стрілкою значення X збільшується, а значення Y зменшується. Якщо ми перейдемо за 90 градусів, X почне зменшуватися, а Y - збільшуватися. Це поведінка і дає нам поворот.

Точки на одиничному колі також відомі під назвами синус і косинус. Тому для будь-якого заданого кута ми можемо отримати значення синуса і косинуса наступним чином:

function printSineAndCosineForAnAngle (angleInDegrees) {var angleInRadians = angleInDegrees * Math.PI / 180; var s = Math.sin (angleInRadians); var c = Math.cos (angleInRadians); console.log ( "s =" + s + "c =" + c); }

Якщо ви скопіюєте код і вставите його в консоль JavaScript, а потім введете printSineAndCosignForAngle (30), то ви побачите s = 0.49 c = 0.87 (я округлив значення).

Якщо скласти все разом, ми можемо повертати геометрію на будь-який заданий кут. Просто встановіть обертанню значення синуса і косинуса кута, на який потрібно виконати поворот.

... var angleInRadians = angleInDegrees * Math.PI / 180; rotation [0] = Math.sin (angleInRadians); rotation [1] = Math.cos (angleInRadians);

Ось версія, де задається кут повороту. Використовуйте слайдери для перенесення або повороту.

Сподіваюся, я доніс сенс. Такий спосіб завдання повороту не є загальноприйнятим, тому продовжуйте читання, ми дійдемо до пункту призначення через дві статті. Наступна буде простіше - масштабування .

Що таке радіани?

Радіани - це одиниці виміру, використовувані при роботі з колами, поворотами і кутами. Як відстань вимірюється в дюймах, ярдів, метрах, так і кути можуть вимірюватися в градусах або радіанах.

Як ви знаєте, з метричними величинами працювати простіше, ніж з імперськими величинами. Потрібно розділити на 12, щоб отримати фути з дюймів. Для перекладу дюймів в ярди потрібно розділити на 36. Не знаю як ви, а я не можу ділити на 36 в розумі. З метричними величинами все набагато простіше. Для перекладу міліметрів в сантиметри ми ділимо на 10. Для перекладу з міліметрів в метри ми ділимо на 1000. На 1000 я можу розділити в умі.

Схожа ситуація у випадку з радіанами і градусами. З градусами працювати складніше. У окружності 360 градусів і тільки 2π радіан. Повне коло 2π радіан. Половина кола - 1π радіан. 1/4 кола, тобто 90 градусів, це 1 / 2π радіан. Тому якщо вам потрібно виконати поворот на 90 градусів, просто використовуйте значення Math.PI * 0.5. Для 45 градусів значення радіанів дорівнюватиме Math.PI * 0.25 і т.д.

Практично вся математика, пов'язана з кутами, колами і поворотами, стане дуже простий, якщо ви будете думати в радіанах. Спробуйте. Використовуйте радіани, а не градуси, за винятком відображення в інтерфейсі.